In the given figure, ABC is a triangle in which AB=AC and D is a point on AB. Through D, a line DE is drawn parallel to BC and meeting AC at E. Prove that AD=AE.

Question

Philoid · Accepted Answer

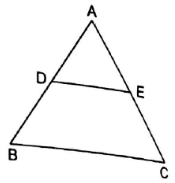
Given that AB = AC and also DE || BC.

So by Basic proportionality theorem or Thales theorem,

=

∴ =

Now adding 1 on both sides,

+ 1 = + 1

=

= … as AB = AD + DE and AC = AE + EC

But is given that AB = AC,

∴ =

Hence,

AD = AE.