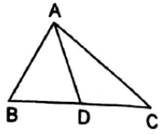
Given: AC>AB and ∠BAD = ∠DAC

To prove: ∠ADC>∠ADB

Proof:

Since AC > AB

∠ABC > ∠ACB

Adding ∠A on both sides

∠ABC + ∠A > ∠ACB + ∠A

∠ABC + ∠BAD > ∠ACB + ∠DAC … As AD is a bisector of ∠A

∴ ∠ADC > ∠ADB