Given: O is a point within ∆ABC

To prove:

(i) AB+AC>OB+OC

(ii) AB+BC+CA>OA+OB+OC

(iii) OA+OB+OC>(AB+BC+CA)

Proof:

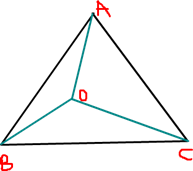
In ∆ABC,

AB +AC >BC ….(1)

And in ∆OBC,

OB + OC > BC …(2)

Subtracting 1 from 2 we get,

(AB + AC) – (OB + OC ) > (BC – BC )

Ie AB + AC > OB + OC

From ׀, AB + AC > OB + OC

Similarly, AB + BC > OA + OC

And AC + BC > OA + OB

Adding both sides of these three inequalities, we get,

(AB + AC ) + (AB + BC) + (AC + BC) > (OB + OC) + (OA + OC) + (OA + OB)

Ie. 2(AB + BC + AC ) > 2(OA + OB + OC)

∴ AB + BC + OA > OA + OB + OC

In ∆OAB,

OA + OB > AB …(1)

In ∆OBC,

OB + OC > BC …(2)

In ∆OCA

OC + OA > CA …(3)

Adding 1,2 and 3,

(OA + OB) + (OB + OC) + (OC+ OA) >AB + BC +CA

Ie. 2(OA + OB + OC) > AB + BC + CA
∴ OA + OB + OC > ( AB + BC + CA)