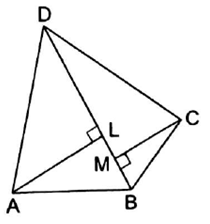
Given :

AL ⊥ BD and CM ⊥ BD

To prove : ar (quad. ABCD) = x BD x (AL + CM)

Proof:

Area of ABD = x BD x AM

Area of ABD = x BD x CM

Now area of Quad ABCD = Area of ABD + Area of BCD

= x BD x AL + x BD x CM

= x BD x (AL + CM)

Hence proved