In the adjoining figure, ABCD is a trapezium in which AB ‖ DC and its diagonals AC and BD intersect at O. Prove that ar(∆AOD) = ar(∆BOC).

Question

In the adjoining figure, ABCD is a trapezium in which AB &#x2016; DC and its diagonals AC and BD intersect at O. Prove that ar(&#x2206;AOD) = ar(&#x2206;BOC).

Philoid · Accepted Answer

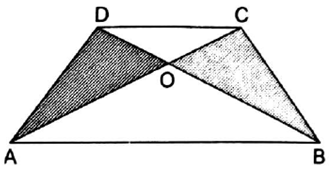
Given

AB ‖ DC

To prove that: area(∆AOD) = area(∆BOC)

Here in the given figure Consider ABD and ABC,

we find that they have same base AB and lie between two parallel lines AB and CD

According to the theorem: triangles on the same base and between same parallel lines have equal areas.

Area of ABD = Area of BCA

Now,

Area of AOD = Area of ABD - Area of AOB ---1

Area of COB = Area of BCA - Area of AOB ---2

From 1 and 2

We can conclude that area(∆AOD) = area(∆BOC) (Since Area of AOB is common)

Hence proved