ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD. Prove that ar(∆BED) = ar(∆ABC).

Question

ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD. Prove that ar(&#x2206;BED) = ar(&#x2206;ABC).

Philoid · Accepted Answer

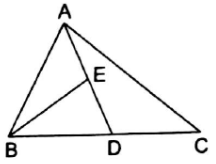
Given : A ∆ABC in which AD is the median and E is the midpoint on line AD

To prove: area(∆BED) = area(∆ABC)

Proof : here in ∆ABC AD is the midpoint

Area of (∆ABD) = Area of (∆ADE)

Hence Area of (∆ABD) = [Area of (∆ABC)] ------------------ 1

No in ∆ABD E is the midpoint of AD and BE is the median

Area of (∆BDE) = Area of (∆ABE)

Hence Area of (∆BED) = [Area of (∆ABD)] -------------- 2

Substituting (1) in (2), we get

Hence Area of (∆BED) = [ Area of (∆ABC)]

area(∆BED) = area(∆ABC)

Hence proved