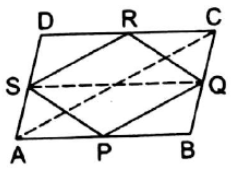
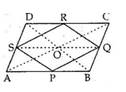
Given : ABCD is a parallelogram and P,Q,R,S are the midpoints of AB,BC,CD,AD respectively

To prove: (i) PQRS is a parallelogram

(ii) Area(‖gm PQRS) = x area(‖gm ABCD)

Construction : Join AC ,BD,SQ

Proof:

(i)

As S and R are midpoints of AD and CD respectively, in ∆ACD

SR || AC [By midpoint theorem] ------------------- (1)

Similarly in ∆ABC , P and Q are midpoints of AB and BC respectively

PQ || AC [By midpoint theorem] ------------------ (2)

From (1) and (2)

SR || AC || PQ

SR || PQ ------------------- (3)

Again in ∆ACD as S and P are midpoints of AD and CB respectively

SP || BD [By midpoint theorem] ------------------ (4)

Similarly in ∆ABC , R and Q are midpoints of CD and BC respectively

RQ || BD [By midpoint theorem] -------------------- (5)

From (4) and (5)

SP || BD || RQ

SP || RQ ----------- (6)

From (3) and (6)

We can say that opposite sides are Parallel in PQRS

Hence we can conclude that PQRS is a parallelogram.

(ii)

Here ABCD is a parallelogram

S and Q are midpoints of AD and BC respectively

SQ || AB

SQAB is a parallelogram

Now, area(∆SQP) = x area of (SQAB) -------------- 1

[Since ∆SQP and ||gm SQAB have same base and lie between same parallel lines]

Similarly

S and Q are midpoints of AD and BC respectively

SQ || CD

SQCD is a parallelogram

Now, area(∆SQR) = x area of (SQCD) ------------------- 2

[Since ∆SQR and ||^gm SQCD have same base and lie between same parallel lines]

Adding (1) and (2) we get

area(∆SQP) + area(∆SQR) = x area of (SQAB) + x area of (SQCD)

area(PQRS) = (area of (SQAB) + area of (SQCD))

Area(‖gm PQRS) = x area(‖gm ABCD)

Hence proved