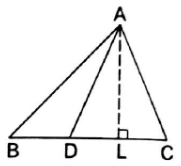
Given : A ∆ABC in which a point D divides the Side BC in the ratio m:n.

To prove: area(∆ABD): area(∆ABC) = m:n

Construction : Drop a perpendicular AL on BC

Proof:

area(∆ABD) = x BD x AL ---------------- (1)

and, area(∆ADC) = x DC x AL ------------------ (2)

BD:DC = m:n

--------------(3)

sub Eq (3) in eq (1)

area(∆ABD) = x ( x DC) x AL

area(∆ABD) = x ( x DC x AL)

area(∆ABD) = x area(∆ADC)

=

Area(∆ABD): Area(∆ABC) = m:n

Hence proved