In a circle of radius 5 cm, 
and 
are two parallel chords of lengths 8 cm and 6 cm respectively. calculate the distance between the chords if they are
(i) on the same side of the center
(ii) on the opposite sides of the center.
(i)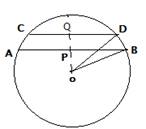 
Let radius OB = OD = 5 cm
Chord AB = 8 cm
Chord CD = 6 cm
BP = (1/2) AB
⇒ BP = (1/2) 8 = 4 cm
DQ = (1/2) CD
⇒ DQ = (1/2) 6 = 3 cm
In triangle OPB,
OP2 = OB2 - BP2
⇒ OP2 = 52 - 42
⇒ OP2= 25 - 16
⇒ OP2= 9
⇒ OP = 3 cm
In triangle OQD,
OQ2 = OD2 - DQ2
⇒ OQ2 = 52 - 32
⇒ OQ2= 25 - 9
⇒ OQ2= 16
⇒ OQ = 4 cm
Now,
PQ = OQ – OP = 4 – 3 = 1
Hence, distance between chords = 1 cm.
(ii)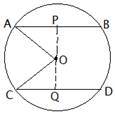 
Let radius OA = OC = 5 cm
Chord AB = 8 cm
Chord CD = 6 cm
AP = (1/2) AB
⇒ AP = (1/2) 8 = 4 cm
CQ = (1/2) CD
⇒ CQ = (1/2) 6 = 3 cm
In triangle OAP,
OP2 = OA2 - AP2
⇒ OP2 = 52 - 42
⇒ OP2= 25 - 16
⇒ OP2= 9
⇒ OP = 3 cm
In triangle OQD,
OQ2 = OC2 - CQ2
⇒ OQ2 = 52 - 32
⇒ OQ2= 25 - 9
⇒ OQ2= 16
⇒ OQ = 4 cm
Now,
PQ = OP + OQ = 3 + 4 = 7
Hence, distance between chords = 7 cm.