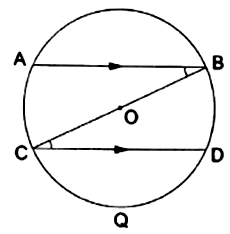
In the adjoining figure, 
is a diameter of a circle with center 
If 
and 
are two chord such that 
prove that 
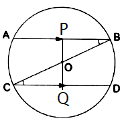
Draw, OP
AB and OQ
CD
In triangle OBP and triangle OQC,
∠OPB = ∠OQC [Angle = 90°]
∠OBP = ∠OCD [Alternate angle]
OB = OC [Radius]
By side-angle-side criterion of congruence
ΔOBP ≅ ΔOQC
∴ OP = OQ
The chords equidistant from the center are equal.
∴ AB = CD Proved.
18