(i) In Figure (1), ![]() is the center of the circle. If
is the center of the circle. If ![]() and
and ![]() find
find ![]() (ii) In figure (2),
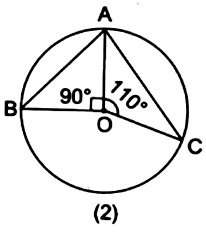
(ii) In figure (2), ![]() and
and ![]() are three points on the circle with center
are three points on the circle with center ![]() such that
such that ![]() and
and ![]() Find
Find ![]()
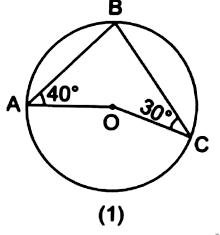
(i) Join OB.
∠OAB = ∠OBA = 40°[Because OB = OA]
∠OCB = ∠OBC = 30°[Because OB = OC]
∠ABC = ∠OBA + ∠OBC
⇒ ∠ABC = 40°+ 30°
⇒ ∠ABC = 70°
∠AOC = 2 × ∠ABC
⇒ ∠AOC = 2 × ∠ABC
⇒ ∠AOC = 2 × 70°
⇒ ∠AOC = 140°
(ii) ![]()
∠BOC = 360° - (∠AOB + ∠AOC) [Sum of all angles at a point = 360°]
⇒ ∠BOC = 360° - (90° + 110°)
⇒ ∠BOC = 360° - 200°
⇒ ∠BOC = 160°
We know that ∠BOC = 2 × ∠BAC
⇒ ∠BAC = (1/2) × ∠BOC
⇒ ∠BAC = (1/2) × 160°
⇒ ∠BAC = 80°
1