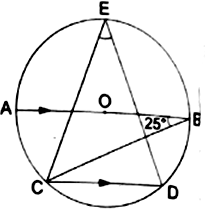
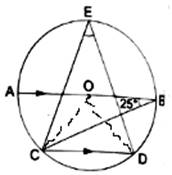
Join OC and OD.

∠ABC = ∠BCD = 25°[Alternate angles]

The angle subtended by an arc of a circle at the center is double the angle subtended by the arc at any point on the circumference.

∴ ∠BOD = 2 × ∠BCD

⇒ ∠BOD = 2 × 25°

⇒ ∠BOD = 50°

Similarly,

∠AOC = 2 × ∠ABC

⇒ ∠AOC = 2 × 25°

⇒ ∠AOC = 50°

Now,

∠AOB = 180° [AOB is a straight line]

⇒ ∠AOC + ∠COD + ∠BOD = 180°

⇒ 50° + ∠COD + 50° = 180°

⇒ 100° + ∠COD = 180°

⇒ ∠COD = 80°

∴∠CED = (1/2) ∠COD

⇒ ∠CED = (1/2) 80°

⇒ ∠CED = 40°