In the given figure, ![]() is the center of a circle in which
is the center of a circle in which![]() and
and ![]() Find (i)
Find (i) ![]() (ii)
(ii) ![]()
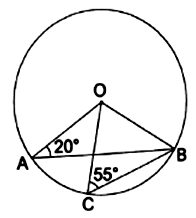
(i) ![]()
OB = OC [Radius]
∴ ∠OBC = ∠OCB = 55°
In triangle OCB,
∠OBC + ∠OCB + ∠BOC = 180°[Sum of angles of triangle]
⇒ 55° + 55° + ∠BOC = 180°
⇒ 110° + ∠BOC = 180°
⇒ ∠BOC = 70°
(ii) ![]()
OA = OB [Radius]
∴ ∠OBA = ∠OAB = 20°
In triangle AOB,
∠OBA + ∠OAB + ∠AOB = 180°[Sum of angles of triangle]
⇒ 20° + 20° + ∠AOB = 180°
⇒ 40° + ∠AOB = 180°
⇒ ∠AOB = 140°
∴ ∠AOC = ∠AOB - ∠BOC
⇒ ∠AOC = 140° - 70°
⇒ ∠AOC = 70°
12