is an isosceles triangle in which If and are midpoints of and respectively, prove that the points are concyclic.

Question

Philoid · Accepted Answer

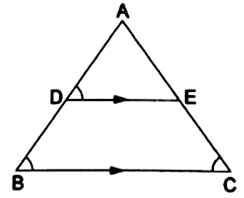
Given, ABC is an isosceles triangle in which AB = AC. D and E are midpoints of AB and AC respectively.

∴ DE || BC

⇒ ∠ADE = ∠ABC ______________ (i)

AB = AC

⇒ ∠ABC = ∠ACB ______________ (ii)

Now,

∠ADE + ∠EDB = 180°[Because ADB is a straight line]

⇒ ∠ACB + ∠EDB = 180°

The opposite angles are supplementary.

∴ D, B, C, E are concyclic.