In the given figure, 
and 
are two parallel chords of a circle. If 
and 
are straight lines, intersecting at 
prove that 
is isosceles.
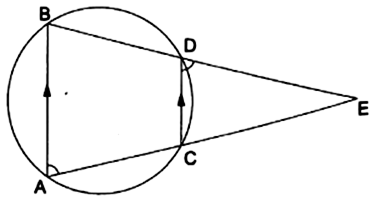
Given: AB and CD are two parallel chords of a circle.
If one side of a cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle.
∴ ext. ∠DCE = ∠B and ext. ∠EDC = ∠A
A || B
∴ ∠EDC = ∠B and ∠DCE = ∠A
∴∠A = ∠B
Hence, ΔAEB is isosceles.
28