State ‘True’ or ‘false’: (i) A triangle can have two right angles. (ii) A triangle cannot have two obtuse angles. (iii) A triangle cannot have two acute angles. (iv) A triangle can have each angle less than 60°. (v) A triangle can have each angle equal to 60°. (vi) There cannot be a triangle whose angles measure 10°, 80° and 100°.

Question

State &#x2018;True&#x2019; or &#x2018;false&#x2019;: (i) A triangle can have two right angles. (ii) A triangle cannot have two obtuse angles. (iii) A triangle cannot have two acute angles. (iv) A triangle can have each angle less than 60&#xB0;. (v) A triangle can have each angle equal to 60&#xB0;. (vi) There cannot be a triangle whose angles measure 10&#xB0;, 80&#xB0; and 100&#xB0;.

Philoid · Accepted Answer

(i) False

Because, sum of angles of triangle equal to 180°.In a triangle maximum one right angle.

(ii) True

Because, obtuse angle measures in 90° to 180° and we know that the sum of angles of triangle is equal to 180°.

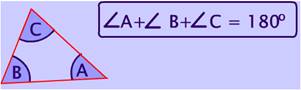
(iii) False

Because, in an obtuse triangle is one with one obtuse angle and two acute angles.

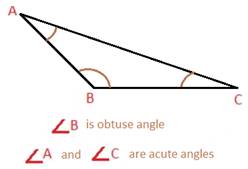
(iv) False

If each angles of triangle is less than 180° then sum of angles of triangle are not equal to 180°.

Any triangle,

∠1 + ∠2 + ∠3 = 180°

(v) True

If value of angles of triangle is same then the each value is equal to 60°.

∠1 + ∠2 + ∠3 = 180°

⇒ ∠1 + ∠1 + ∠1 = 180°[∠1 = ∠2 = ∠3]

⇒ 3 ∠1 = 180°

⇒ ∠1 = 60°

(vi) True

We know that sum of angles of triangle is equal to 180°.

Sum of angles,

= 10° + 80° + 100°

= 190°

Therefore, angles measure in (10°, 80°, 100°) cannot be a triangle.