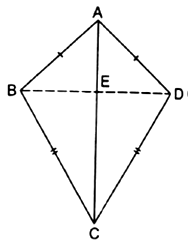
Given: In ABCD, and

To prove: (i) bisects and

(ii)

(iii)

Proof:

(i) In ∆ABC and ∆ADC, we have,
AB = AD …given

BC = DC …given
AC = AC … common side
Hence, by SSS congruence rule,

∆ABC ≅ ∆ADC

∴ ∠BAC = ∠DAC and ∠BCA = ∠D​CA …By cpct
Thus, AC bisects ∠A and ∠ C.
(ii) Now, in ∆ABE and ∆ADE, we have,

AB = AD …given​
∠BAE = ∠DAE​ …from i
AE = AE …common side
Hence, by SAS congruence rule,

∆ABE ≅ ∆ADE
∴ BE = DE …by cpct
(iii) ∆ABC ≅ ∆ADC from ii

∴ ∠ABC = ∠AD​C …by cpct