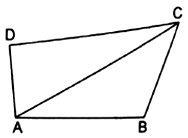
Given: In ABCD, AC is one of diagonals.

To prove:

(i)

(ii)

(iii)

Proof:

(i) We know that the sum of any two sides of a triangle is greater than the third side.
In ∆ABC,

AB + BC > AC ...(1)

In ∆ACD,

CD + DA > AC ...(2)

​Adding (1) and (2), we get,

AB + BC + CD + DA > 2AC

(ii) In ∆ABC, we have,
AB + BC > AC ...(1)
We also know that the length of each side of a triangle is greater than the positive difference of the length of the other two sides.
In ∆ACD, we have:​
AC > DA – CD ...(2)
From (1) and (2), we have,
AB + BC > DA − CD
∴ AB + BC + CD > DA

(ii) In ∆ABC,

AB + BC > AC …(1)

In ∆ACD,

CD + DA > AC …(2)

In ∆ BCD,

BC + CD > BD …(3)

In ∆ ABD,

DA + AB > BD …(4)
​Adding 1, 2, 3 and 4, we get,
2(AB + BC + CD + DA) > 2(AC + BD)
∴ AB + BC + CD + DA > AC + BD