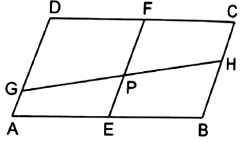
Here, ABCD is parallelogram.

By the properties of parallelogram,

AD || BC and AB || DC

AD = BC and AB = DC

Also,

AB = AE + BE and DC = DF + FC

This means that,

AE = BE = DF = FC

Now, DF = AE and DF || AE, that is AEFD is a parallelogram​​.

Hence, AD || EF​

Similarly, ​BEFC is also a parallelogram.

Hence, EF || BC
∴​ AD || EF || BC

Thus, AD, EF and BC are three parallel lines cut by the transversal line DC at D, F and C, respectively such that DF = FC.

Also, the lines AD, EF and BC​ are also cut by the transversal AB at A, E and B, respectively such that​ AE = BE. ​
Similarly, they are also cut by​ GH.

Hence by intercept theorem,
∴ GP = PH

Hence proved.