In the adjoining figure, ![]() and
and ![]() are the medians of
are the medians of ![]() and
and ![]() Show that
Show that ![]()
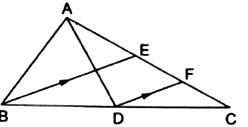
Here in ![]() AD and BE are medians.
AD and BE are medians.
Hence, in ∆ABC, we have:
AC = AE + EC
But AE = EC … as E is midpoint of AC
∴ AC = 2EC …(1)
Now in ∆BEC,
DF || BE
Also, EF = CF … by midpoint theorem, as D is the midpoint of BC
But,
EC = EF + CF
∴ EC = 2 CF …(2)
From 1 and 2, we get,
AC = 4 CF
∴ ![]()
5