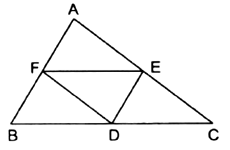
Here, in , are the midpoints of the sides and respectively.

By mid point theorem, as F and E are the mid points of sides AB and AC,

FE ∣∣ BC

Similarly, DE ​∣∣ FB and FD ​∣∣ AC.

Therefore, AFDE, BDEF and DCEF are all parallelograms.

We know that opposite angles in parallelogram are equal.

∴ In AFDE, we have,

∠A = ∠EDF

In BDEF, we have,

∠B = ∠DEF

In DCEF, we have,

∠ C = ∠​ DFE

Hence proved.