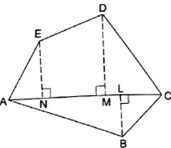
Given: A pentagon ABCDE

and

cm

cm

cm

cm

cm

cm

MC = AC – AM = 18 – 14 = 4 cm

MN = AM – AN = 14 – 6 = 8 cm

Here,

Area (Pent. ABCDE) = area (AEN) + area (DMC) + area (ABC) + area (Trap. DMNE)

Area of triangle = × (base) × (height).

Area of trapezium is × (sum of parallel sides) × height

Here,

Area (AEN) = × (AN) × (EN) = × (6) × (9) = 27 cm².

Area (DMC) = × (MC) × (DM) = × (4) × (12) = 24 cm².

Area (ABC) = × (AC) × (BL) = × (18) × (4) = 36 cm².

Area (Trap. DMNE) = × (DM + EN) × MN = × (12 + 9) × 8 = 84 cm².

Area (Pent. ABCDE) = area (AEN) + area (DMC) + area (ABC) + area (Trap. DMNE)

= 27 + 24 + 36 + 84 = 171 cm².

Area (Pent. ABCDE) = 171 cm^2.