(i) Given pair of linear equations is

3x - y - 5 = 0 …(i)

and 6x - 2y - p = 0 …(ii)

On comparing with ax + by + c = 0 we get

Here, a₁ = , b₁ = - 1, c₁ = - 5;

And a₂ = 6, b₂ = - 2, c₂ = - p;

a₁ /a₂ = /6 = 1/2

b₁ /b₂ = 1/2

c₁ /c₂ = 5/p

Since, the lines represented by these equations are parallel, then

a₁/a₂ = b₁/b₂ c₁/c₂

Taking last two parts, we get

So, p

Hence, the given pair of linear equations are parallel for all real values of p except 10 i.e.,

P

(ii) Given pair of linear equations is

- x + py = 1 …(i)

and px - y - 1 = 0 …(ii)

On comparing with ax + by + c = 0, we get

Here, a₁ = , b₁ = p, c₁ =- 1;

And a₂ = p, b₂ = - 1, c₂ =- 1;

a₁ /a₂ =

b₁ /b₂ = - p

c₁ /c₂ = 1

Since, the lines equations has no solution i.e., both lines are parallel to each other.

a₁/a₂ = b₁/b₂ c₁/c₂

= - p 1

Taking last two parts, we get

p

Taking first two parts, we get

p² = 1

p = 1

Hence, the given pair of linear equations has no solution for p = 1.

(iii) Given, pair of linear equations is

- 3x + 5y = 7

and 2px - 3y = 1

On comparing with ax + by + c = 0, we get

Here, a₁ = , b₁ = 5, c₁ = - 7;

And a₂ = 2p, b₂ = - 3, c₂ = - 1;

a₁ /a₂ =

b₁ /b₂ = - 5/3

c₁ /c₂ = 7

Since, the lines are intersecting at a unique point i.e., it has a unique solution

a₁/a₂ b₁/b₂

so,

p 9/10

Hence, the lines represented by these equations are intersecting at a unique point for all real values of p except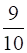

(iv) Given, pair of linear equations is

2x + 3y - 5 = 0

and px - 6y - 8 = 0

On comparing with ax + by + c = 0 we get

Here, a₁ = , b₁ = 3, c₁ = - 5;

And a₂ = p, b₂ = - 6, c₂ = - 8;

a₁ /a₂ =

b₁ /b₂ = - 3/6 = - 1/2

c₁ /c₂ = 5/8

Since, the pair of linear equations has a unique solution.

a₁/a₂ b₁/b₂

so - 1/2

p - 4

Hence, the pair of linear equations has a unique solution for all values of p except - 4

i.e., p

(v) Given pair of linear equations is

2x + 3y = 7

and 2px + py = 28 - qy

or 2px + (p + q)y - 28 = 0

On comparing with ax + by + c = 0 we get

Here, a₁ = , b₁ = 3, c₁ = - 7;

And a₂ = 2p, b₂ = (p + q), c₂ = - 28;

Since, the pair of equations has infinitely many solutions i.e., both lines are coincident.

a₁/a₂ = b₁/b₂ = c₁/c₂

= =

Taking first and third parts, we get

p = 4

Again, taking last two parts, we get

=

p + q = 12

Since p = 4

So, q = 8

Here, we see that the values of p = 4 and q = 8 satisfies all three parts.

Hence, the pair of equations has infinitely many solutions for all values of p = 4 and q = 8.