Given pair of equations is

x + y = 3 …(i)

and 3x + 3y = 9 …(ii)

On comparing with ax + by + c = 0

Here, a₁ = 1, b₁ = 1, c₁ = - 3;

And a₂ = 3, b₂ = 3, c₂ = - 9;

a₁ /a₂ = 1/3

b₁ /b₂ = 1/3

c₁ /c₂ = 1/3

Here, a₁/a₂ = b₁/b₂ = c₁/c₂, i.e. coincident lines

Hence, the given pair of linear equations is coincident and having infinitely many solutions.

The given pair of linear equations is consistent.

Now,

If x = 0 then y = 3, If x = 3, then y = 0.

and

If x = 0 then y = 3, if x = 1, then y = 2, and if x = 3, then y = 0.

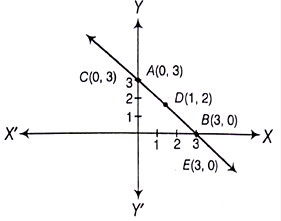
Plotting the points A(0, 3) and B(3, 0), we get the line AB. Again, plotting the points C(0, 3) and D(1, 2) and E(3, 0), we get the line CDE.