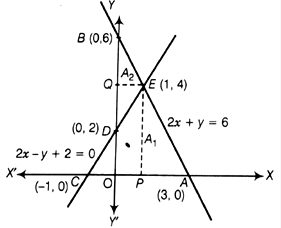
Graphically, solve the following pair of equations

2x + y = 6 and 2x – y + 2 = 0


Find the ratio of the areas of the two triangles formed by the lines representing these equations with the X - axis and the lines with the Y - axis.

Given equations are 2x + y = 6 and 2x – y + 2 = 0

Table for equation 2x + y - 6 = 0, for x = 0, y = 6, for y = 0, x = 3.


x



0



3



y



6



0



Points



B



A



Table for equation 2x – y + 2 = 0, for x = 0, y = 2, for y = 0,x = - 1


x



0



- 1



y



2



0



Points



D



C



Let A1 and A2 represent the areas of and & respectively where E is the intersection of lines.



Now, Area of triangle formed with x -axis =



=


And Area of triangle formed with y - axis =





Hence, the pair of equations intersect graphically at point E(1,4)


i.e., x = 1 and y = 4.


1