Given equation is - 4 + (- 1) + 2 + - - - + x = 437

Its terms can be listed as

- 4, - 1, 2, - - - , x

And this is an AP with First term, a = - 4

Common difference, d = - 1 - (- 4) = 3

Let the no of terms be n

Then Sum of first n terms, S_n = 437

n[ 2 (- 4) + (n - 1)3] = 874

n (- 8 + 3n - 3) = 874

n(3n - 11) = 874

3n² - 11n - 874 = 0

Solving this quadratic equation with

A = 3

B = - 11

C = - 874

Then D = b² - 4ac = (- 11)² - 4(3) (- 874)

= 121 + 10488 = 10609

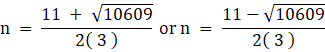
(not possible as n is a natural no)

so x is the 19^th term of AP

x = a₁₉ = a + 18d

= - 4 + 18(3)

= 50