If AOBC is a rectangle whose three vertices are A (0, 3), O (0, 0) and B (5, 0), then the length of its diagonal is
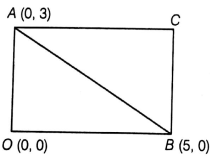
We have three vertices;
A = (0, 3)
O = (0, 0)
B = (5, 0)
Now,
As we know that diagonals of a rectangle are of equal length,
So,
Length of the diagonal AB = Distance between the points A and B
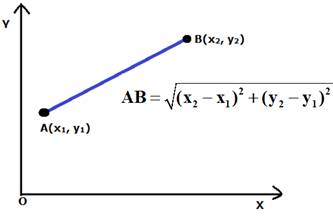
Calculate the distance between the points (x1, y1) and (x2, y2);
By the formula;
We have;
d2 = (x2 - x1)2 + (y2 - y1)2
x1 = 0, x2 = 5
y2 = 3, y2 = 0
d2 = (5 – 0)2 + (0 – 3)2
![]()
d = √(25 + 9)= √34
Distance between A (0, 3) and B (5, 0) is √34
Hence, the required length of its diagonal is √34
7