Given a parallelogram ABCD whose three vertices are;

A ( - 2, 3),

B (6, 7) and

C (8, 3)

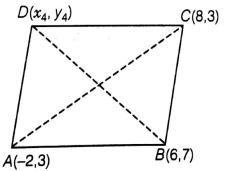
Let the fourth vertex of parallelogram, D = (x₄, y₄) and L, M be the middle points of AC and BD, respectively

L =

Since, mid - point of a line segment having points (x₁, y₁) and (x₂, y₂)

= and

M =

As we know ABCD is a parallelogram, therefore diagonals AC and BD will bisect each other.

So, L and M are the same points

3 = and

3 =

→ 6 = 6 + x₄ and 6 = 7 + y₄

→ x₄ = 0 and y₄ = 6 – 7

∴ x₄ = 0 and y₄ = - 1

Hence, the fourth vertex of parallelogram is D = (x4, y4) = (0, 1)