First, we have to plot the points of the line segment on the paper and join them.

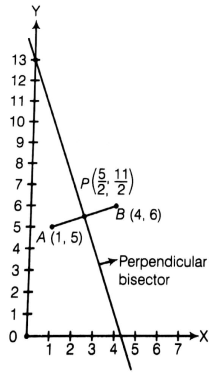
As we know that the perpendicular bisector of line segment AB, perpendicular at AB and passes through the mid - point of AB.

Let P be the mid - point of AB

Now find the mid - point,

Mid - point of AB =

_∵ Mid - point of line segment passes through the points (x₁, y₁) and (x₂, y₂)

=

Find the slope of the bisector:

Slop of the given line =

Slope =
Slope of given line multiplied by slope of bisector = - 1
Slope of bisector =
= - 3
Find out the bisector's formula by using the point slope form;

Which is;
- 3 =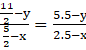

- 3(2.5 – x) = 5.5 - y
- 7.5 + 3x = 5.5 - y
3x + y - 13 = 0
Transform the formula into slope - intercept form
3x + y - 13 = 0
y = - 3x + 13
because slope - intercept form is y = mx + c,

Where, m is the slope and c is the y - intercept
Thus, perpendicular bisector cuts the y - axis at (0, 13)

So, the required point is (0, 13).