ΔABC with vertices A(0 - 2, 0), B(2, 0) and C(0, 2) is similar to ΔDEF with vertices D( - 4, 0), E(4, 0) and F(0, 4).

Question

Philoid · Accepted Answer

True

Given,

ΔABC = ΔDEF

Now,

Calculate the distance between A (2, 0) and B (2, 0) in ΔABC;

∵ Distance between the points (x₁, y₁) and (x₂, y₂);

So,

Similarly, distance between B (2, 0) and C (0, 2)

Distance between C (0, 2) and A (2, 0)

Now,

Calculate the distance between F (0, 4) and D ( - 4, 0) in ΔDEF;

Distance between F (0, 4) and E ( - 4, 0);

Distance between E (4, 0) and D ( - 4, 0);

Now,

Here, we see that sides of ΔABC and ΔFDE are proportional.

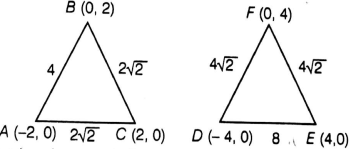
Hence, both the triangles are similar by SSS rule.