Firstly, we plot the points of the line segment on the paper and join them.

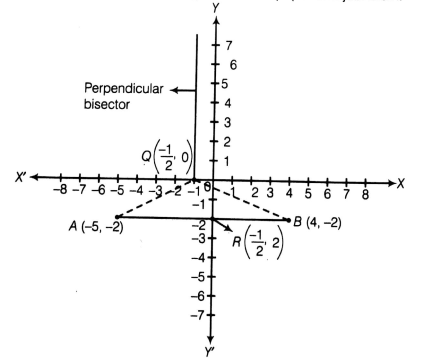
We know that, the perpendicular bisector of the line segment AB passes through the mid - point of AB and divide the line in two equal parts.

Mid - point of a line segment passes through the points (x₁ + x₂) and (y₁ + y₂) is;

Mid - point of (x₁ + x₂) and (y₁ + y₂) =

So,

Mid - point of AB =

R =

Now, we draw a straight line on paper passes through the mid - point R.

We see that perpendicular bisector cuts the X - axis at the point Q

So, the coordinates of the point Q is on the X - axis which lies on the perpendicular bisector of the line segment joining the point AB.

To know the type of triangle formed by the points Q, A and B,

We have to find out the length of all three sides and see whatever condition of triangle is satisfied by these sides.

Now, using distance formula between two points (x₁, y₁) and (x₂, y₂);

d =

So,

AB = = 9

BQ =

QA =

We see that, BQ = QA ≠ AB

Which shows that the triangle formed by the points Q, A and B is an isosceles.