Let three vertices of the triangle be A, B and C

And the coordinates of third vertex be (x, y)

We have,

A ( - 4, 3),

B (4, 3) and

C (x, y)

We know that, in equilateral triangle the angle between two adjacent sides is 60 and all three sides are equal.

∴ AB = BC = CA

→ AB² = BC² = CA²

Now, taking first two parts

AB² = BC²

(4 + 4)² + (3 - 3)² = (x – 4)² + (y – 3)²

64 + 0 = x² + 16 – 8x + y² + 9 – 6y

x² + y² – 8x – 6y = 39……. (ii)

Now, taking first and third parts;

AB² = CA²

(4 + 4)² + (3 - 3)² = ( - 4 - x)² + (3 – y)²

64 + 0 = 16 + x² + 8x + 9 + y² – 6y

x² + y² + 8x – 6y = 39……. (iii)

On subtracting Eq. (ii) from Eq. (iii),

We get:

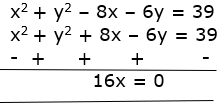
→ x = 0

Now, by putting the value of x in Eq. (ii),

We get;

0 + y² – 0 – 6y = 39

→ y² – 6y – 39 = 0

∴ y =

∵ Solution of ax² + bx + c = 0 is x =

y =

So, the points of third vertex are (0,3 + 4√3) or (3 - 4√3)

But given that, the origin lies in the interior of the ΔABC and the x - coordinate of third vertex is zero.

Then, y - coordinate of third vertex should be negative.

Hence, the required coordinate of third vertex,

C = [∵ c ≠ ]