The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ΔABC.

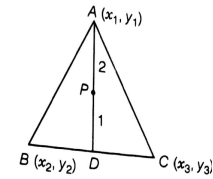
(i) The median from A meets BC at D. Find the coordinates of the point D.


(ii) Find the coordinates of the point P on AD such that AP: PD = 2: 1.


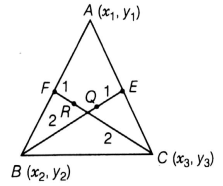
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ: QE = 2:1 and CR: RF = 2: 1.


(iv) What are the coordinates of the centroid of the ΔABC?

Given,

The vertices of ΔABC = A, B and C


Coordinates of A, B and C;


A(x1, y1)


B(x2, y2)


C(x3, y3)


(i) As per given information D is the mid - point of BC and it bisect the line into two equal parts.


Coordinates of the mid - point of BC;


BC –



(ii) Let the coordinates of a point P be (x, y)



Given,


The point P(x, y), divide the line joining A(x1, y1) and D in the ratio 2:1


Then,


Coordinates of P =


By using internal section formula;


=



(iii) ∴ Let the coordinates of a point Q be (p, q)



Given,


The point Q (p, q),


Divide the line joining B(x2, y2) and E in the ratio 2:1,


Then,


Coordinates of Q =


=


Since, BE is the median of side CA, So BE divides AC in to two equal parts.


∴ mid - point of AC = Coordinate of E;


E =


So, the required coordinate of point Q;


Q =


Now,


Let the coordinates of a point E be (⍺, β)


Given,


Point R (⍺, β) divide the line joining C(x3, y3) and F in the ratio 2:1,


Then the coordinates of R;


=


=


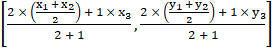
Since, CF is the median of side AB.


So, CF divides AB in to two equal parts.


∴ mid - point of AB = Coordinate of F;


F =


So, the required coordinate of point R;


=


(iv) Coordinate of the centroid of the ΔABC;




3