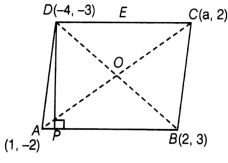
If the points A(1, - 2), B(2, 3), C(a, 2) and D( - 4, - 3) form a parallelogram, then find the value of a and height of the parallelogram taking AB as base.
In parallelogram, we know that, diagonals are bisects each other i.e., mid - point of AC = mid - point of BD
![]()
![]() = - 1
= - 1
Since, mid - point of a line segment having points (x1, y1) and (x2, y2) is ![]()
![]() 1 + a = - 2
1 + a = - 2
![]() a = - 3
a = - 3
So, the value of a is – 3
Given,
AB as base of a parallelogram and drawn a perpendicular from D to AB which meets AB at P.
So, DP is a height of a parallelogram.
Now, equation of base AB, passing through the points (1, - 2) and (2, 3) is;
![]() (y – y1) =
(y – y1) = ![]()
![]() (y + 2) =
(y + 2) = ![]()
![]() (y + 2) = 5(x - 1)
(y + 2) = 5(x - 1)
![]() 5x – y = 7
5x – y = 7
Slop of AB = m1 = ![]() ….. (i)
….. (i)
Let the slope of DP be m2.
Since, DP is perpendicular to AB.
By condition of perpendicularity,
m1.m2 = - 1 ![]() 5.m2 = - 1
5.m2 = - 1
![]() m2 = -
m2 = - ![]()
Now,
Equation of DP, having slope - ![]() and passing the point ( - 4, - 3) is;
and passing the point ( - 4, - 3) is;
(y– y1) = m2(x – x1)
→ (y + 3) = - ![]() (x + 4)
(x + 4)
→ 5y + 15 = - x – 4
→ x + 5y = - 19 ……(ii)
On adding Equations (i) and (ii), then we get the intersection point P.
By putting the value of y from Eq. (i) to Eq. (ii),
We get;
X + 5(5x – 7) = - 19
X + 25x – 35 = - 19
26x = 16
x = ![]()
Put the value of x in Eq. (i);
We get;
y = 5![]()
∴ Coordinates of point P = ![]()
By distance formula,
Distance between two points (x1, y1) and (x2, y2) is;
D = ![]()
So, length of the height of a parallelogram,
DP = ![]()
DP = ![]()
![]()
![]()
![]()
Hence, the required length of height of a parallelogram is ![]()