If the height of a tower and the distance of the point of observation from its foot, both are increased by 10%, then the angle of elevation of its top remains unchanged.
True
Let height of the tower be h and distance of the point from its foot is x.
Let angle of elevation be θ1
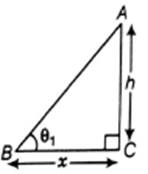
In ![]()
![]() …eq. 1
…eq. 1
Now, when both(height and distance) are increased by ![]() we get
we get
New height = h+10%of h
![]()
![]()
New distance = x+10% of x
![]()
![]()
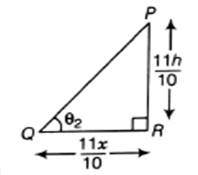
In ∆PQR,
![]()
![]()
From eq.1 and eq.2, we get θ1 = θ2
Hence, it is true.
12