The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 600 and the angle of elevation of the top of the second from the foot of the first tower is 300. Find the top of distance between the two towers and also the height of the tower.
Given that height of one of the tower is 30 m, ∠QAB = 60° and ∠PBA = 30°
Let height of another tower be h m & distance between the towers be x m.
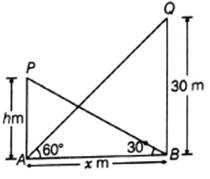
We need to find x and h.
So, in ∆QAB,
![]()
![]()
![]()
& in ∆PBA,
![]()
we have got the value of x, i.e. 10√3 m. So, putting the value of x in the above equation,
![]()
⇒ h = 10
Thus, we have required distance between the towers, i.e. 10√3 m
& height of another tower, i.e. 10 m.
14