Let QO = x and given that BQ = q, such that BO = q+x is the height of the wall.

Let AO = y and given that SA = q.

∠BAO = α and ∠QSO = β

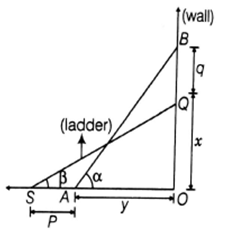
In ∆BAO,

⇒ BO = AB sin α …eq. 1

⇒ AO = AB cos α …eq. 2

In ∆QSO,

⇒ QO = SQ sin β …eq. 3

⇒ SO = SQ cos β …eq. 4

Subtracting eq. 2 from eq. 4, we get

SO –AO = SQ cos β – AB cos α

⇒ SA = SQ cos β – AB cos α

[from the above figure, SO –AO = SA = p]

⇒ p = AB cos β – AB cos α

[∵ SQ=AB=length of the ladder]

⇒ p = AB (cos β – cos α) …eq. 5

And subtracting eq. 3 from eq. 1, we get

BO –QO = AB sin α – SQ sin β

⇒ BQ = AB sin α – SQ sin β

[from the above figure, BO –QO = BQ = q]

⇒ q = AB sin α – AB sin β

[∵ SQ=AB=length of the ladder]

⇒ q = AB (sin α – sin β) …eq. 6

Dividing eq. 5 and eq. 6, we get

Hence, proved.