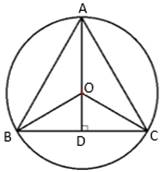
Given: Equilateral triangle of side 9 cm is inscribed in a circle.

Construction: Join OA, OB, OC and drop a perpendicular bisector from center O to BC.

Here,

Area (ΔABC) = 3× area (ΔOBC)

Area (ΔABC) = a² = × 9² =

Now,

Area (ΔOBC) = × AC × OD = × 9 × OD

We know that,

Area (ΔABC) = 3× area (ΔOBC)

= × 9 × OD

OD =

Now, in ΔODC

By Pythagoras theorem

OC² = OD² + DC²

OC² = ² + ²

OC² = + = = 27

OC =

∴ Radius = OC =