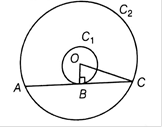
Given : Two circles (say C1 and C2) with common center as O and

Radius of circle C1, r₁ = 4 cm

Radius of circle C2, r₂ = 5 cm

Also say AC is the chord of circle C2 which is tangent to circle C1 and OB is the radius of circle to the point of contact of tangent AC .

To find : Length of chord AC

Now, Clearly OB ⏊ AC [ As tangent to at any point on the circle is perpendicular to the radius through point of contact]

So OBC is a right-angled triangle

So, it will satisfy Pythagoras theorem [ i.e. (base)² + (perpendicular)² = (hypotenuse)² ]

i.e.

(OB)² + (BC)² = (OC)²

As OB and OC are the radii of circle C1 and C2 respectively.

So

(4)² + (BC)² = (5)²

16 + (BC)² = 25

(BC)² = 25 - 16 = 9

BC = 3 cm

Also

AB = BC [ Perpendicular through the center to a chord in a circle (C2 in this case) bisects the chord]

And

AC = AB + BC

= AB + AB = 2AB = 2(3) = 6 cm