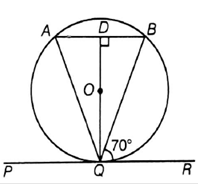
Given : PQR is a tangent to a circle Q with center O and AB is a chord parallel to PR and ∠BQR = 70°

To Find : ∠AQB

Now, ∠OQR = ∠DQR = 90° [ As tangent at any point on the circle is perpendicular to the radius through point of contact]

∠DQR = ∠QBD + ∠BQR

90 = ∠QBD + 70°

∠QBD = 20° [1]

As, AB || PR

∠BDQ + ∠DQR = 180° [ some of co interior angles ]

∠BDQ + 90° = 180°

∠BDQ = 90°

And

∠ADQ + ∠BDQ = 180° [Linear pair]

∠ADQ + 90° = 180°

∠ADQ = 90° = ∠BDQ

In △AQD and △BQD

QD = QD [common]

∠ADQ = ∠BDQ [Proved Above]

AD = BD [since, perpendicular from center to the chord bisects the chord]

△AQD ≅ △BQD [By Side Angle Side Criterion]

And

∠AQD = ∠BQD [ Corresponding parts of congruent triangles are equal ]

∠AQD + ∠BQD = ∠AQB

∠AQB = 2∠BQD [As ∠AQD = ∠BQD ]

∠AQB = 2(20) = 40° [From 1]