If a chord AB subtends an angle of 60° at the center of a circle, then angle between the tangents at A and B is also 60°.

Question

Philoid · Accepted Answer

False

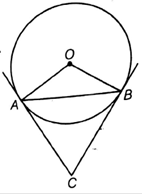
Consider the problem in above diagram. In which we have a circle with center O and AB be any chord with ∠AOB = 60°

Now,

OA ⏊ AC and OB ⏊ CB [ As tangent to at any point on the circle is perpendicular to the radius through point of contact]

∠OBC = ∠OAC = 90° [1]

In Quadrilateral AOBC [ By angle sum property of quadrilateral]

∠OBC + ∠OAC + ∠AOB + ∠ACB = 360°

90° + 90° + 60° + ∠ACB = 360°

∠ACB = 120° [2]

So the angle between two tangents is 120°. So the above statement is false .