True

Consider a figure for the problem in which we have a circle with center O.

PT is a tangent drawn from external point P. Joint OT.

OT ⏊ PT [ As tangent at any point on the circle is perpendicular to the radius through point of contact]

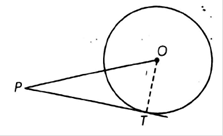
So, OPT is a right-angled triangle formed.

In right angled triangle, hypotenuse is always greater than any of the two sides of the triangle.

So,

OP > PT or PT < OP

Hence, Length of tangent from an external point P on a circle with center O is always less than OP .