True

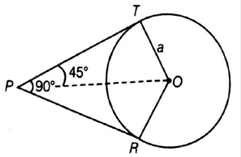
Let us consider a circle with center O and tangents PT and PR and angle between them is 90° and radius of circle is a

To show :

Proof :

In △OTP and △ORP

TO = OR [ radii of same circle]

OP = OP [ common ]

TP = PR [ tangents through an external point to a circle are equal]

△OTP ≅ △ORP [ By Side Side Side Criterion ]

∠TPO = ∠OPR [Corresponding parts of congruent triangles are equal ] [1]

Now, ∠TPR = 90° [Given]

∠TPO + ∠OPR = 90°

∠TPO + ∠TPO = 90° [By 1]

∠TP0 = 45°

Now, OT ⏊ TP [ As tangent at any point on the circle is perpendicular to the radius through point of contact]

∠OTP = 90°

So △POT is a right-angled triangle

And we know that,

So,

[As OT is radius and equal to a]

Hence Proved !