The tangent to the circumcircle of an isosceles Δ ABC at A, in which AB = AC, is parallel to BC.

Question

Philoid · Accepted Answer

True

Let us consider a circle in which EF is a tangent passing through point A on the circle and ABC is an isosceles triangle in the circle , in which AB = AC

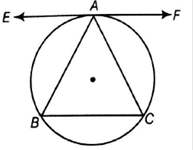
To Prove : EF || BC

Construction : Join OA , OB and OC

Proof :

AB = AC [Given]

∠ACB = ∠ABC [Angles opposite to equal sides are equal] [1]

∠EAB = ∠ACB [Tangents drawn from an external point to a circle are equal] [2]

From [1] and [2]

∠EAB = ∠ACB

i.e. EF || BC [ two lines are parallel if their alternate interior angles are equal]

The tangent to the circumcircle of an isosceles ΔABC at A, in which AB = AC, is parallel to BC.