Two tangents PQ and PR are drawn from an external point to a circle with center O. Prove that QORP is a cyclic quadrilateral.
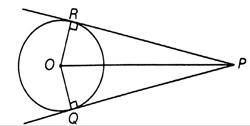
Given : PQ and PR are two tangents drawn at points Q and R are drawn from an external point P .
To Prove : QORP is a cyclic Quadrilateral .
Proof :
OR ⏊ PR and OQ ⏊PQ [Tangent at a point on the circle is perpendicular to the radius through point of contact ]
∠ORP = 90°
∠OQP = 90°
∠ORP + ∠OQP = 180°
Hence QOPR is a cyclic quadrilateral. As the sum of the opposite pairs of angle is 180°
2