Given : AB and CD are two common tangents to two circles of unequal radii.

To Prove : AB = CD

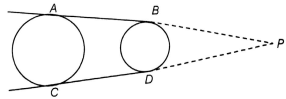
Construction: Produce AB and CD, to intersect at P.

Proof:

Consider the circle with greater radius.

AP = CP [Tangents drawn from an external point to a circle are equal] [1]

Also,

Consider the circle with smaller radius.

BP = BD [Tangents drawn from an external point to a circle are equal] [2]

Substract [2] from [1]. We Get

AP - BP = CP - BD

AB = CD

Hence Proved .