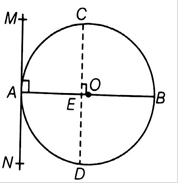
Let AB be diameter in a circle with center O and MN is the chord at point A .

And CD be any chord parallel to MN intersecting AB at E

To Prove : AB bisects CD .

Proof :

OA ⏊ MN [Tangent at a point on the circle is perpendicular to the radius through point of contact ]

∠MAO = 90°

Also, ∠CEO = 90°

[ if E point lies on the OA then by Corresponding angles and if E lies on OB then by sum of co-interior angles ]

So, we have OE ⏊ CD

CE = ED [ Perpendicular drawn from the center of a circle to chord bisects the chord ]

Implies that AB bisects CD

Hence Proved !