Let s denotes the semi-perimeter of a ΔABC in which BC = a, CA = b and AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively. Prove that BD = s – b.
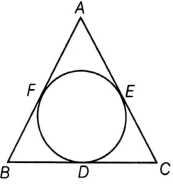
Given : A triangle ABC with BC = a , CA = b and AB = c . Also, a circle is inscribed which touches the sides BC, CA and AB at D, E and F respectively and s is semi- perimeter of the triangle
To Prove : BD = s - b
Proof :
Given that
Semi Perimeter = s
Perimeter = 2s
Implies that
2s = AB + BC + AC [1]
As we know,
Tangents drawn from an external point to a circle are equal
So we have
AF = AE [2] [Tangents from point A]
BF = BD [3] [Tangents From point B]
CD = CE [4] [Tangents From point C]
Adding [2] [3] and [4]
AF + BF + CD = AE + BD + CE
AB + CD = AC + BD
Adding BD both side
AB + CD + BD = AC + BD + BD
AB + BC - AC = 2BD
AB + BC + AC - AC - AC = 2BD
2s - 2AC = 2BD [From 1]
2BD = 2s - 2b [as AC = b]
BD = s - b
Hence Proved !