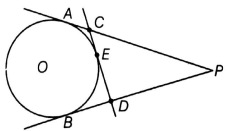
Given : From an external point P, two tangents, PA and PB are drawn to a circle with center O. At a point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. And PA = 10 cm

To Find : Perimeter of △PCD

As we know that, Tangents drawn from an external point to a circle are equal.

So we have

AC = CE [1] [Tangents from point C]

ED = DB [2] [Tangents from point D]

Now Perimeter of Triangle PCD

= PC + CD + DP

= PC + CE + ED + DP

= PC + AC + DB + DP [From 1 and 2]

= PA + PB

Now,

PA = PB = 10 cm as tangents drawn from an external point to a circle are equal

So we have

Perimeter = PA + PB = 10 + 10 = 20 cm