Two circles with centers O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.
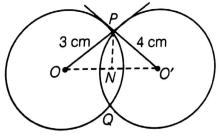
Given : Two circles with centers O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’P are tangents to the two circles and PQ is a common chord.
To Find : Length of common chord PQ
∠OPO' = 90° [Tangent at a point on the circle is perpendicular to the radius through point of contact ]
So OPO is a right-angled triangle at P
Using Pythagoras in △ OPO', we have
(OO')2= (O'P)2+ (OP)2
(OO')2 = (4)2 + (3)2
(OO')2 = 25
OO' = 5 cm
Let ON = x cm and NO' = 5 - x cm
In right angled triangle ONP
(ON)2+ (PN)2= (OP)2
x2 + (PN)2 = (3)2
(PN)2= 9 - x2 [1]
In right angled triangle O'NP
(O'N)2 + (PN)2= (O'P)2
(5 - x)2 + (PN)2 = (4)2
25 - 10x + x2 + (PN)2 = 16
(PN)2 = -x2+ 10x - 9[2]
From [1] and [2]
9 - x2 = -x2 + 10x - 9
10x = 18
x = 1.8
From (1) we have
(PN)2 = 9 - (1.8)2
=9 - 3.24 = 5.76
PN = 2.4 cm
PQ = 2PN = 2(2.4) = 4.8 cm